Jacobiの楕円函数(sn,cn,dn)とEdwards曲線の関係
#数楽 "楕円曲線のEdwards formについて" 作成者:
@genkurokihttps://twitter.com/i/moments/854368021279784960 …
#数楽 メモEdwards curve: x^2+by^2=1+ax^2+y^2これは x^2(1-ay^2)=1-by^2 と同じ。x=u/(1-ay-2)とおくとこれはu^2=(1-ay^2)(1-by^2)と双有理同値。第1種微分はω=dy/u.続く
#数楽 続き。b=1の場合はJacobiの楕円函数の場合。xy座標ではω=dy/(x(1-ay^2))=x dy/(1-by^2).特にa=0, b=1でx^2+y^2=1の場合にはω=dy/x=-dx/y=dθ.ここでx=cos θ, y=sin θ.
#数楽 訂正1-ay-2は訂正容易な自明な誤植。正しくは1-ay^2.https://twitter.com/genkuroki/status/856165230539194368 …
#数楽 続きω=dy/√((1-ay^2)(1-by^2)).b=1, a=k^2と仮定する。θ=∫_0^y ωの逆函数は y=sn θ (Jacobiのsn函数).a=0のときsn θ=sin θ.a=1のときsn θ=tanh θ.続く
#数楽 続き「実xy平面内の実Edwards曲線x^2+y^2=1+ax^2y^2がコンパクトであること」(これは実xy平面内の実Edwards曲線が自然にAbel群になることと同じ)と「a≦0」と「modulus kが純虚数であること」は同値。
#数楽 Jacobiのsn函数の話に戻る。y=sn θで、cn,dn函数は(cn θ)^2=1-y^2(dn θ)^2=1-ay^2を満たし、x^2=(1-y^2)/(1^ay^2)だったのでx=cn θ/dn θ.これがEdwards曲線のパラメーター表示。
#数楽 cn θ/dn θはcd θと書かれるらしい。x=cd θy=sn θとおくとx^2+y^2=1+k^2x^2y^2.k=0のとき、x=cos θy=sin θで普通の三角函数の場合。
#数楽 楕円曲線のEdwards formの加法公式よりci=cd θisi=sn θiε=c1c2s1s2とおくとcd(θ1+θ2)=(c1c2-as1s2)/(1-aε)sn(θ1+θ2)=(c1s2+s1c2)/(1+aε).続く
#数楽 Jacobiの楕円函数達の加法公式の導出は実は結構面倒(教科書によってはテータ函数による表示とテータ函数の加法公式に帰着していたりする。複素解析的にやるならテータ函数がとても便利)。Edwards formを利用すると、計算量が減り、証明も代数的に初等的になると思う。
#数楽 楕円曲線のEdwards formを知る前には、正直なはなし「snなどのJacobiの楕円函数にはあんまりさわりたくない。全部テータ函数でやった方がずっと超」と思っていたが、知ってからはJacobiの楕円函数への抵抗がかなり減った。
#数楽 実Edwards曲線の形を見たい人は https://www.geogebra.org/m/XjJ2yPhp を見て下さい。Edwards曲線には効率的で安全度の高い楕円曲線暗号への応用があるので、文化的に抵抗感が薄れるべき曲線の一つになっています。群としての円の直接的一般化。
#数楽 Edwards曲線の話はJacobiの楕円函数論のいちバージョンに過ぎないとみなせるのですが、例外のないシンプルな公式の追求が実用面で大きな価値を持っていることを示しています。良い公式は計算量を減らし、セキュリティを増すことになる!
#数楽 ところで、高校生向けの数学の参考書の類が文科省が決めた学習指導要領やら伝統的に受験数学とみなされる事柄に過剰適応している様子はちょっと異様。楕円曲線や楕円函数のようなネタは数学の研究的にも実用的にも価値が高いので、もっと普通の定番のネタになってもいいような感じがします。
#数楽 補足:楕円函数の有理点のなす群が無限遠点を含むと、コンピューターで計算するとき、分母が0になるケースを例外扱いしなければいけなくなります。例外的なケースでの消費電力の変化などの計測によって、セキュリティが突破され易くなります。Edwards曲線ではそれを避けられます。続く
#数楽 続き。Edwards曲線の加法公式は、オイラー、ガウス、ヤコビらによる楕円函数の研究にルーツがあります。オイラーさんもガウスさんもヤコビさんも自分の研究にこんな応用があることを想像することさえできてなかったはずです。

#数楽 Jacobiの楕円函数sn,cn,dnの加法公式とEdwards曲線x^2+y^2=1+k^2x^2y^2の加法公式の関係1/2pic.twitter.com/80JNfF6OvF

#数楽 Jacobiの楕円函数sn,cn,dnの加法公式とEdwards曲線x^2+y^2=1+k^2x^2y^2の加法公式の関係2/2pic.twitter.com/CG2NQXuNa9
#数楽 "Jacobiの楕円函数(sn,cn,dn)とEdwards曲線の関係"https://twitter.com/i/moments/856359432405393408 …
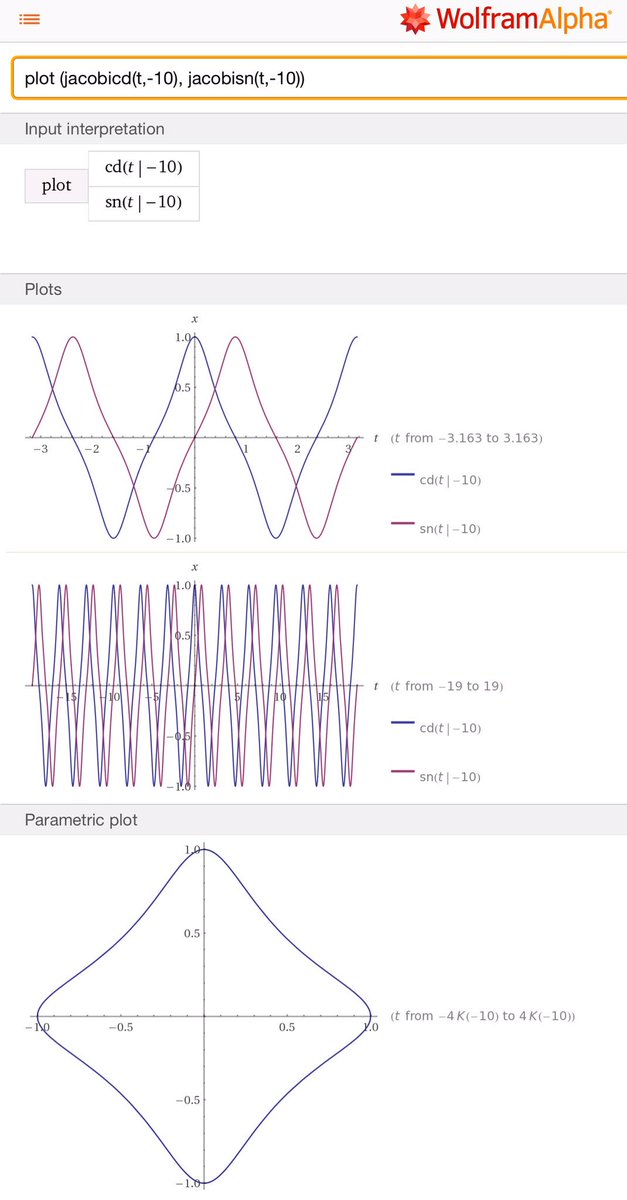
#数楽 ヤコビの楕円函数sn tとcd t=cn t/dn tによる(cd t, sn t)の軌跡はEdwards曲線x^2+y^2=1+k^2x-2y^2になる。添付画像はk^2=-10の場合。http://www.wolframalpha.com/input/?i=plot%20(jacobicd(t,-10), jacobisn(t,-10)) …pic.twitter.com/de2QlZ0Y44
#数楽 k^2=0のときx^2+y^2=1の円になり、cd t=cos t, sn t=sin tとなる。一般のk^2でも、cos,sinの関係と同じように、cd tはsn tの「位相」をずらして得られる函数になる。cd,snの組はcos,sinの組の自然な一般化だと思える。
#数楽 楕円曲線暗号に応用されているEdwards曲線の加法公式はヤコビの楕円函数(cd t, sn t)=(cn t/dn t, sn t)の加法公式に一致する。ヤコビさんは約200年後に自分の名のついた楕円函数の加法公式がこんな形で応用されるとは思って無かっただろう。
#数楽 訂正Edwards曲線の正しい式はx^2+y^2=1+k^2 x^2 y^2で、これはx^2(1-k^2y^2)=1-y^2と同値。z=x(1+k^2y^2)とおくとz^2=(1-y^2)(1-k^2y^2)https://twitter.com/genkuroki/status/856405471824986112 …
#数楽 楕円曲線のEdwards formをx^2=(1-y^2)/(1-k^2y^2)と書くとJacobi formz^2=(1-y^2)(1-k^2y^2)との違いは1-k^2y^2が分母分子のどちらにあるか。Edwards formはxとyについて対称である。
#数楽 気分的には、(x,y)=(cos θ, sin θ)と同じ程度に、(x,y)=(cd θ, sn θ)に親しみを感じていいんじゃないかと思うようになった。三角函数と比較するとヤコビの楕円函数の方がずっと計算が複雑になるのですが。
#数楽 個人的には、純代数的にやれるケースであっても、微積分を使える場合についてのヴァリエーションがどうなっているかについても知りたくなるタイプ。自分が定義した量子τがそうなっていない点は結構不満かも。
#数楽 検索メモhttps://www.google.co.jp/search?q=Ed25519 …Ed25519を検索。Ed25519のEdはEdwardsのEdです。結構お世話になっている人達がいるはず。
#数楽 結構お世話になっている人達がいるはずのEdwards曲線の加法公式が実はヤコビの楕円函数(cd t, sn t)の加法公式に本質的に一致しているという話がこの発言の返答連鎖の内容です。ヤコビの楕円函数が間接的にこんな形で役に立っていたとはびっくり。
#数楽 sin tの自然な拡張がsn tなのはいいとして、cos tの拡張としてcn tではなくて、cd t=cn t/dn tを考えた方が対称性が高まって少し楽をできるというようなことは、ずっと知らなかった。cd tという記号法も知らなかった。
#数楽 Edwards曲線の加法公式が暗号に応用されるときには離散的な環境で利用されるのですが、離散的な場合に役に立つ公式が離散的な場合だけを扱っていて発見されたとは全く思えないわけで、オイラー、ガウス、ヤコビによる楕円積分と楕円函数の研究が重要だったわけです。
http://sync.twi2mstdn.space のテスト。例えば、#数楽 Ed25519のお世話になっている人は、そっちで使われているのは捻られたEdwards曲線だけど、加法公式の形は捻っていないx^2+y^2=1+k^2x^2y^2のケースとほぼ同じなので、続く
http://sync.twi2mstdn.space のテスト続き#数楽 続き〜、ヤコビの楕円函数による(x,y)=(cd t, sn t) (最初はk^2=-10とかにしておく)をプロットするとEdwards曲線が得られることを知っておくと親しみがわきやすくなるかも。続く
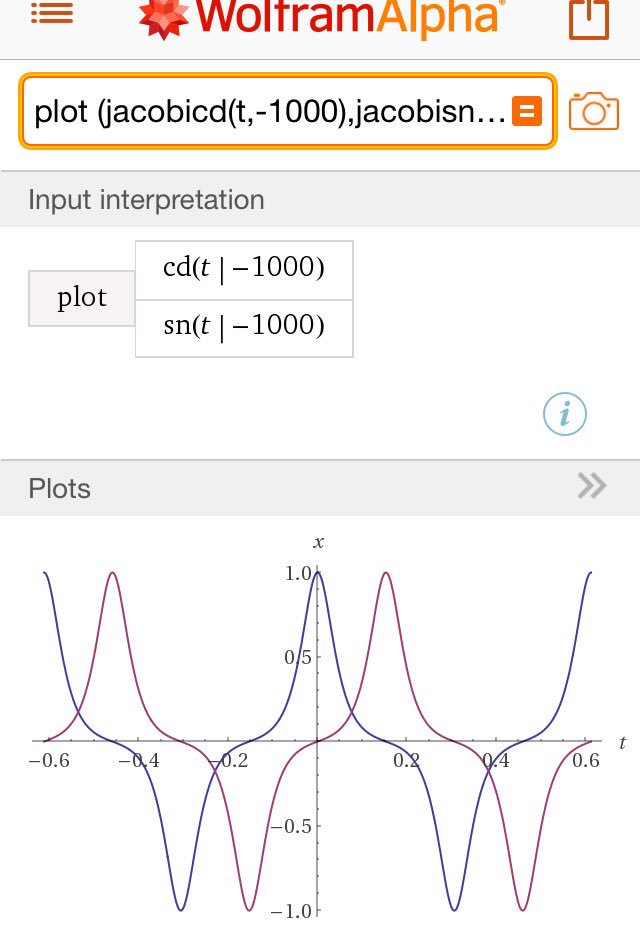
#数楽 ヤコビの楕円函数のプロットはWolframAlphaを使えば一発でできる。cd(t|k^2),sn(t|k^2)はjacobicd(t,k^2),jacobisn(t,k^2).http://www.wolframalpha.com/input/?i=plot%20(jacobicd(t,-1000),jacobisn(t,-1000)) …pic.twitter.com/o0rV8DpWRB
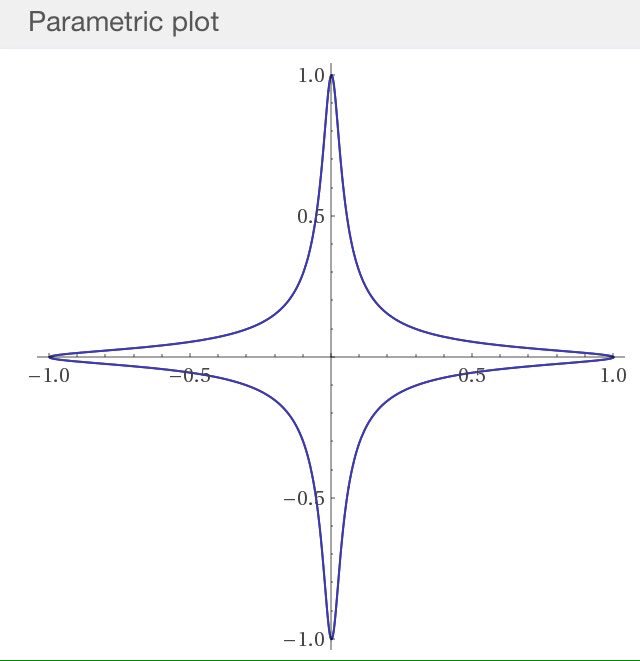
#数楽 スクショの続き。(x,y)=(cd t, sn t)をプロットとするとEdwards曲線x^2+y^2=1+k^2x^2y^2が得られます。添付画像はk^2=-1000の場合。pic.twitter.com/sJvJRNsY3C
#数楽 函数や曲線の様子を見たければまず最初にWolframAlphaを使うのがよいと思う。数学的に初等的はケースではGeoGebraも便利。何も知らない状態から数時間あればリンク先のようなことができます。 https://www.geogebra.org/m/XjJ2yPhp
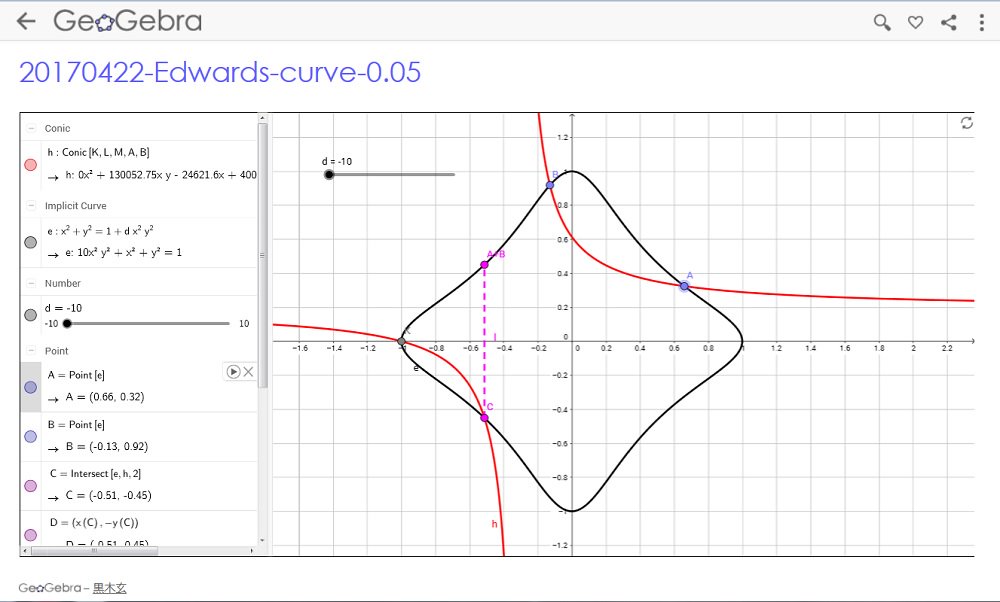
#数楽 GeoGebraを使った楕円曲線のEdwards formの加法公式のプロットの例のスクリーンショット(GeoGebraについて何も知らなくても数時間あればこの程度の初等的なことなら可能)https://www.geogebra.org/m/XjJ2yPhp pic.twitter.com/dC4PG1cm9H
#数楽 続き。私は初めて触るこの手の道具を平均より早く使える方だと思う。それにもかかわらず、数時間かけてその程度のことしかできないとも言える。GeoGebraのような道具は、数学を教える側ではなく、教わる側が使用しなければ教育的効果は小さいと思うのですが、現実は厳しいかも。
#数楽 ヤコビの楕円函数sn,cn,dnよりも、データ函数が好きという話の続き。テータ函数は色々扱い易い函数です。Mumfordさんの論文や本にあるようにテータ函数を使った楕円曲線のモデルは良いモデルだろうと予想できるわけです。暗号にも応用あるんじゃないかと思ったら〜続く
#数楽 続き〜すでにそういう研究がされていました。普通テータ函数で一度は考えるよなあという感じの論文。2013年版には文献表が見当たらないので2013年版も引用。https://pdfs.semanticscholar.org/100c/fce4ccdc90ac3cc2c6eca63c41b3fc82793a.pdf …http://eprint.iacr.org/2012/346.pdf
#数楽 一つ前の論文はテータ函数から得られた公式を任意標数に適用するという話。テータ函数達はsn,cn,dn函数達よりやはり扱い易いと思う。ヤコビさんは楕円函数をテータ函数の商で書いており、Θ(テータ)とH(エータ)という記号を使っていた。
#数楽 訂正2013年版の新しい方だけではなく、2012年版も引用。https://twitter.com/genkuroki/status/857203519526285312 …
#数楽 訂正:なぜか「テータ函数」ではなく、「データ函数」と書いてあった。もちろん「テータ函数」が正しい。https://twitter.com/genkuroki/status/857202837079474177 …
#数楽 テータ函数の解説については例えば David Mumford, Tata Lectures on Theta I,II,III を http://www.dam.brown.edu/people/mumford/alg_geom/abelian.html … の下の方からダウンロードできます。楕円曲線の付随するテータ函数の解説はIにあります。
#数楽 Mumford's Tata Lectures on Theta のPDFsへの直接リンクI→ http://www.dam.brown.edu/people/mumford/alg_geom/papers/Tata1.pdf …II→ http://www.dam.brown.edu/people/mumford/alg_geom/papers/Tata2.pdf …III→ http://www.dam.brown.edu/people/mumford/alg_geom/papers/Tata3.pdf …
#数楽 I,IIはTeX化されていないので分量的にはページ数のわりにそう多くはないと考えられます。MumfordのTata Lectures on Theta I,IIは非常に面白いです。様々な数学が関係する楽しい話がたくさん書いてあります。

#数楽 ただし、数式に細かい誤りがあるので自分で訂正しながら読む必要があります。大抵の数学の本はそういうもの。理解できているかどうかは自力で訂正できるかで判断できる。例えば添付画像のように虚数単位のiが抜けているところがある。pic.twitter.com/U8jKzjL4XK

#数楽 たぶん https://en.wikipedia.org/wiki/Theta_function … は Mumford, Tata Lectures on Theta Iの流儀を採用してる。添付画像とWikipediaの対応箇所を比較してみて下さい。pic.twitter.com/U8jKzjL4XK
#数楽 テータ函数についてはhttp://www.ac.cyberhome.ne.jp/~narukawa/index-j.html …からダウンロードできる成川淳「テータ関数の不思議な公式」もおすすめします。楕円テータ函数をexp(積分)の形で表わしておいて、モジュラー変換公式を留数計算だけで証明する方法が書いてあります。



